Last edited:
In the introductory article, I provided a comprehensive summary of the challenge. The story turned out to be rather long and a bit half-baked: it did not contain a single line of code.
However, it’s hard to talk about specific optimizations without the preceding summary. Of course, one can apply some techniques to any code at hand. For instance, caching calculations or reducing branching. But I believe certain things can not be done without an overall understanding of the problem you’re dealing with. That is what distinguishes a living person from the optimizing compiler. And, that’s why manual optimizations still play a critical part: compilers deal with code, humans handle problems. A compiler can not decide a number is sufficiently random while a human can.
The eternal problem of a real random number choosingLet us recall we’re talking about optimizing image resize via convolution-based resampling in the Pillow Python library. In this “general optimizations” article I’m going to tell you about the changes I implemented several years ago. It’s not a word-for-word story: I optimized the order of optimizations for the narrative. I also created a separate branch of version 2.6.2 in the repo, that’s our starting point.
If you’d like this to get interactive and not just read but run some tests, here’s the pillow-perf repo. Feel free to install the deps and run the tests by yourself:
# Installing packages needed for compiling and testing
$ sudo apt-get install -y build-essential ccache python-dev libjpeg-dev
$ git clone -b opt/scalar https://github.com/uploadcare/pillow-simd.git
$ git clone --depth 10 https://github.com/python-pillow/pillow-perf.git
$ cd ./pillow-simd/
# Swithching to the commit everything starts with
$ git checkout bf1df9a
# Building and setting up Pillow
$ CC="ccache cc" python ./setup.py develop
# Finally, running the test
$ ../pillow-perf/testsuite/run.py scale -n 3Because Pillow consists of many modules and can’t be compiled incrementally, we use the ccache utility to speed up repetitive builds significantly.
pillow-perf allows you to test many different operations, but we’re interested in the scale specifically where -n 3 sets the number of test runs. While the code is pretty slow, let’s use the smaller number of -n not to fall asleep. Here are the results for the initial performance, commit bf1df9a:
Operation Time Bandwidth
---------------------------------------------
to 320x200 bil 0.08927 s 45.88 Mpx/s
to 320x200 bic 0.13073 s 31.33 Mpx/s
to 320x200 lzs 0.16436 s 24.92 Mpx/s
to 2048x1280 bil 0.40833 s 10.03 Mpx/s
to 2048x1280 bic 0.45507 s 9.00 Mpx/s
to 2048x1280 lzs 0.52855 s 7.75 Mpx/s
to 5478x3424 bil 1.49024 s 2.75 Mpx/s
to 5478x3424 bic 1.84503 s 2.22 Mpx/s
to 5478x3424 lzs 2.04901 s 2.00 Mpx/sAs you might remember, the tests show scaling of a 2560×1600 RGB image.
The results above differ from the official ver. 2.6 benchmark performance. There are two reasons for that:
A significant part of the code we’re about to look into is in the Antialias.c file, the ImagingStretch function exactly. The code of the function can be split into three parts:
// Prelude
if (imIn->xsize == imOut->xsize) {
// Vertical resize
} else {
// Horizontal resize
}As I highlighted in the previous article, convolution-based resize can be done in two passes: the first one deals with changing image width, and the second one — with height or vice versa.
The ImagingStretch function deals with one of the dimensions in one call.
Here, you can see the function is called twice for every resize operation. Firstly, there goes a prologue and then one or another operation depending on the input parameters. Quite an unusual way to get rid of the repeating code: prologue in this case. Within the function, both passes look similar adjusted to the processing direction. For brevity, here’s the code for one of the passes:
for (yy = 0; yy < imOut->ysize; yy++) {
// Counting the coefficients
if (imIn->image8) {
// A single 8-bit channel loop
} else {
switch (imIn->type) {
case IMAGING_TYPE_UINT8:
// Loop, multiple 8-bit channels
case IMAGING_TYPE_INT32:
// Loop, single 32-bit channel
case IMAGING_TYPE_FLOAT32:
// Loop, single float channel
}
}
}We can see the branching for picture formats supported by Pillow: single-channel 8-bit, shades of gray; multi-channel 8-bit, RGB, RGBA, LA, CMYK, and others; single-channel 32-bit and 32-bit float. We’re specifically interested in the multi-channel 8-bit format since it’s the most common image format.
Even though I mentioned the two passes look similar, there’s a significant difference. Let’s check out the vertical pass first:
for (yy = 0; yy < imOut->ysize; yy++) {
// Calculating coefficients
for (xx = 0; xx < imOut->xsize*4; xx++) {
// Convolution, column of pixels
// Saving pixel to imOut->image8[yy][xx]
}
}And the horizontal one:
for (xx = 0; xx < imOut->xsize; xx++) {
// Calculating coefficients
for (yy = 0; yy < imOut->ysize; yy++) {
// Convolution, row of pixels
// Saving pixel to imOut->image8[yy][xx]
}
}While in the vertical pass we iterate through the columns of the resulting image, in the horizontal one we deal with rows. The horizontal pass is then a serious problem for the processor cache. Each step of the embedded cycle accesses one lower row thus requesting a value that is far from the value needed for the previous step.
That’s a problem when working with smaller-sized convolution. The thing is, current processors are only capable of reading a 64-byte cache line from RAM. This means when we convolve less than 16 pixels, reading some part of the data from RAM to cache is a waste. But imagine we inverted the loops. Now, each convolved pixel is not in the next row but the next pixel of the current row. Hence, most of the needed pixels would already be in the cache.
The second negative factor of such code organization relates to a long convolution line: in the case of a significant downscaling. The thing is, for the adjacent convolutions the original pixels intersect significantly, and it would be great if these data remained in the cache. But when we move from top to bottom, the data for the old convolutions are gradually being replaced from the cache by the data for the new ones. As a result, after the embedded loop when the next external step begins, there are no upper rows in the cache, they are all replaced by the lower ones. Hence, we must read those upper rows from RAM again. And when it comes to the lower rows, all the data have already been replaced by the higher rows in the cache. It turns out a loop where none of the needed data are ever in the cache.
Why is it so? In the pseudo code above we see that the second line in both cases stands for the calculation of the convolution coefficients. For the vertical pass, coefficients only depend on the yy values in a row of the resulting image, and for the horizontal — on the xx values in the current column. Hence, we can’t just swap the two loops in the horizontal pass: we should calculate the coefficients inside the loop for xx. If we start counting the coefficients in the embedded loop, we get a degrade in performance. Especially when we use the Lanczos filter for the calculations: it makes use of trigonometric functions.
So, we shouldn’t calculate the coefficients on every step even though those are identical for every pixel in a column. However, we can calculate coefficients for all the columns in advance and use them in the embedded loop. Let’s do this.
There’s a line for allocating the memory for coefficients:
k = malloc(kmax * sizeof(float));Now, we’ll need an array of such arrays. We can simplify through allocating a flat memory fragment and emulating two dimensions via addressing:
kk = malloc(imOut->xsize * kmax * sizeof(float));We’ll also need a storage for xmin and xmax which also depend on xx. Let’s make an array for those:
xbounds = malloc(imOut->xsize * 2 * sizeof(float));Also inside the loop, a value of ww is used for normalizing, ww = 1 / Σk. We do not need to store it at all. Instead, we can normalize the coefficients themselves, and not convolution results. So, once we calculate the coefficients, we iterate through them again dividing every single value by the coefficients sum. As a result, the sum of all the coefficients becomes 1.0:
k = &kk[xx * kmax];
for (x = (int) xmin; x < (int) xmax; x++) {
float w = filterp->filter((x - center + 0.5) * ss);
k[x - (int) xmin] = w;
ww = ww + w;
}
for (x = (int) xmin; x < (int) xmax; x++) {
k[x - (int) xmin] /= ww;
}Finally, we can rotate the process by 90 degrees:
// Calculating the coefficients
for (yy = 0; yy < imOut->ysize; yy++) {
for (xx = 0; xx < imOut->xsize; xx++) {
k = &kk[xx * kmax];
xmin = xbounds[xx * 2 + 0];
xmax = xbounds[xx * 2 + 1];
// Convolution, row of pixels
// Saving pixel to imOut->image8[yy][xx]
}
}Here are the performance results we get then, commit d35755c:
Operation Time Bandwidth Improvement
-------------------------------------------------------------
to 320x200 bil 0.04759 s 86.08 Mpx/s 87.6 %
to 320x200 bic 0.08970 s 45.66 Mpx/s 45.7 %
to 320x200 lzs 0.11604 s 35.30 Mpx/s 41.6 %
to 2048x1280 bil 0.24501 s 16.72 Mpx/s 66.7 %
to 2048x1280 bic 0.30398 s 13.47 Mpx/s 49.7 %
to 2048x1280 lzs 0.37300 s 10.98 Mpx/s 41.7 %
to 5478x3424 bil 1.06362 s 3.85 Mpx/s 40.1 %
to 5478x3424 bic 1.32330 s 3.10 Mpx/s 39.4 %
to 5478x3424 lzs 1.56232 s 2.62 Mpx/s 31.2 %The fourth column shows the performance improvements.
In some parts of the code we can see such construction:
if (ss < 0.5)
imOut->image[yy][xx*4+b] = (UINT8) 0;
else if (ss >= 255.0)
imOut->image[yy][xx*4+b] = (UINT8) 255;
else
imOut->image[yy][xx*4+b] = (UINT8) ss;The snippet is about limiting pixel values in the 8-bit range of [0, 255] in case the calculation results are outside of it. That can happen because the sum of all the positive convolution coefficients can be greater than one, and the sum of all the negative ones can be less than zero. So, we can sometimes stumble upon an overflow. The overflow is the result of compensating for sharp brightness gradients and is not an error.
Let’s take a look at the code. There’s one input variable ss and a single output imOut-> image[yy]. The output gets assigned values in several places. The thing here is we’re comparing floating point numbers while it would be more efficient to convert values into integers and then perform the comparison. So this is the function:
static inline UINT8
clip8(float in) {
int out = (int) in;
if (out >= 255)
return 255;
if (out <= 0)
return 0;
return (UINT8) out;
}Usage:
imOut->image[yy][xx*4+b] = clip8(ss);This optimization also gives us a boost in performance, a moderate one this time, commit 54d3b9d:
Operation Time Bandwidth Improvement
-----------------------------------------------------------
to 320x200 bil 0.04644 s 88.20 Mpx/s 2.5 %
to 320x200 bic 0.08157 s 50.21 Mpx/s 10.0 %
to 320x200 lzs 0.11131 s 36.80 Mpx/s 4.2 %
to 2048x1280 bil 0.22348 s 18.33 Mpx/s 9.6 %
to 2048x1280 bic 0.28599 s 14.32 Mpx/s 6.3 %
to 2048x1280 lzs 0.35462 s 11.55 Mpx/s 5.2 %
to 5478x3424 bil 0.94587 s 4.33 Mpx/s 12.4 %
to 5478x3424 bic 1.18599 s 3.45 Mpx/s 11.6 %
to 5478x3424 lzs 1.45088 s 2.82 Mpx/s 7.7 %As you can see, this optimization has a greater effect on filters with smaller windows and larger output resolutions with the only exception of 320×200 Bilinear; I did not research why it worked out this way. That’s reasonable, the smaller the filter window and the larger the final resolution, the greater our value limiting contributes to the overall performance.
If we, again, look through the code for the horizontal pass, we encounter four inner loops:
for (yy = 0; yy < imOut->ysize; yy++) {
// ...
for (xx = 0; xx < imOut->xsize; xx++) {
// ...
for (b = 0; b < imIn->bands; b++) {
// ...
for (x = (int) xmin; x < (int) xmax; x++) {
ss = ss + (UINT8) imIn->image[yy][x*4+b] * k[x - (int) xmin];
}
}
}
}We’re iterating through every row and column of the output image: every pixel, to be precise. Embedded loops are there to iterate through every pixel of the input image to be convolved. What about b? It’s there to iterate through the bands of your image. It’s quite obvious the number of image bands is rather constant and does not exceed four: due to the way Pillow represents images.
Hence, there are four possible cases, one of which deals with single-channel 8-bit images. Those are represented differently thus the final number of cases is three. We can now make three separate inner loops: for 2-, 3-, and 4-band images respectively. Then, we add branching to switch between the modes. Here’s the code for the most common case of a 3-band image, not to take much space here:
for (xx = 0; xx < imOut->xsize; xx++) {
if (imIn->bands == 4) {
// Body, 4-band images
} else if (imIn->bands == 3) {
ss0 = 0.0;
ss1 = 0.0;
ss2 = 0.0;
for (x = (int) xmin; x < (int) xmax; x++) {
ss0 = ss0 + (UINT8) imIn->image[yy][x*4+0] * k[x - (int) xmin];
ss1 = ss1 + (UINT8) imIn->image[yy][x*4+1] * k[x - (int) xmin];
ss2 = ss2 + (UINT8) imIn->image[yy][x*4+2] * k[x - (int) xmin];
}
ss0 = ss0 * ww + 0.5;
ss1 = ss1 * ww + 0.5;
ss2 = ss2 * ww + 0.5;
imOut->image[yy][xx*4+0] = clip8(ss0);
imOut->image[yy][xx*4+1] = clip8(ss1);
imOut->image[yy][xx*4+2] = clip8(ss2);
} else {
// Body, 1- and 2-band images
}
}We can go even further and unwrap the branching one more time, to the cycle for xx:
if (imIn->bands == 4) {
for (xx = 0; xx < imOut->xsize; xx++) {
// Body, 4 channels
}
} else if (imIn->bands == 3) {
for (xx = 0; xx < imOut->xsize; xx++) {
// Body, 3 channels
}
} else {
for (xx = 0; xx < imOut->xsize; xx++) {
// Body, 1 and 2 channels
}
}Here’s what performance improvements we get, commit 95a9e30:
Operation Time Bandwidth Improvement
-----------------------------------------------------------
to 320x200 bil 0.03885 s 105.43 Mpx/s 19.5 %
to 320x200 bic 0.05923 s 69.15 Mpx/s 37.7 %
to 320x200 lzs 0.09176 s 44.64 Mpx/s 21.3 %
to 2048x1280 bil 0.19679 s 20.81 Mpx/s 13.6 %
to 2048x1280 bic 0.24257 s 16.89 Mpx/s 17.9 %
to 2048x1280 lzs 0.30501 s 13.43 Mpx/s 16.3 %
to 5478x3424 bil 0.88552 s 4.63 Mpx/s 6.8 %
to 5478x3424 bic 1.08753 s 3.77 Mpx/s 9.1 %
to 5478x3424 lzs 1.32788 s 3.08 Mpx/s 9.3 %Something similar can be found for the vertical pass. Here’s the initial code:
for (xx = 0; xx < imOut->xsize*4; xx++) {
/* FIXME: skip over unused pixels */
ss = 0.0;
for (y = (int) ymin; y < (int) ymax; y++)
ss = ss + (UINT8) imIn->image[y][xx] * k[y-(int) ymin];
ss = ss * ww + 0.5;
imOut->image[yy][xx] = clip8(ss);
}There’s no iterating through channels. Instead, xx iterates over the width multiplied by four, i.e., xx goes through each channel no matter the number of bands in an image. FIXME in the comment relates to that fix. We’re doing the same: adding branching to switch depending on the number of input image bands. The code can be found in the commit f227c35, here are the results:
Operation Time Bandwidth Improvement
-----------------------------------------------------------
to 320x200 bil 0.03336 s 122.80 Mpx/s 16.5 %
to 320x200 bic 0.05439 s 75.31 Mpx/s 8.9 %
to 320x200 lzs 0.08317 s 49.25 Mpx/s 10.3 %
to 2048x1280 bil 0.16310 s 25.11 Mpx/s 20.7 %
to 2048x1280 bic 0.19669 s 20.82 Mpx/s 23.3 %
to 2048x1280 lzs 0.24614 s 16.64 Mpx/s 23.9 %
to 5478x3424 bil 0.65588 s 6.25 Mpx/s 35.0 %
to 5478x3424 bic 0.80276 s 5.10 Mpx/s 35.5 %
to 5478x3424 lzs 0.96007 s 4.27 Mpx/s 38.3 %I’d like to highlight that the horizontal pass optimizations provide better performance for downscaling an image while the vertical pass — for upscaling.
for (y = (int) ymin; y < (int) ymax; y++) {
ss0 = ss0 + (UINT8) imIn->image[y][xx*4+0] * k[y-(int) ymin];
ss1 = ss1 + (UINT8) imIn->image[y][xx*4+1] * k[y-(int) ymin];
ss2 = ss2 + (UINT8) imIn->image[y][xx*4+2] * k[y-(int) ymin];
}If we take a look at the embedded loop, we can see that ymin and ymax are declared as floats. However, those are converted to integers at every step. Moreover, outside the loop, when the variables get assigned any values, floor and ceil functions are used. So, every value they ever get assigned is an integer even though the variables are initially declared as floats. The same concept can be applied to xmin and xmax. Let’s change that and check out the performance, commit 57e8925:
Operation Time Bandwidth Improvement
-----------------------------------------------------------
to 320x200 bil 0.03009 s 136.10 Mpx/s 10.9 %
to 320x200 bic 0.05187 s 78.97 Mpx/s 4.9 %
to 320x200 lzs 0.08113 s 50.49 Mpx/s 2.5 %
to 2048x1280 bil 0.14017 s 29.22 Mpx/s 16.4 %
to 2048x1280 bic 0.17750 s 23.08 Mpx/s 10.8 %
to 2048x1280 lzs 0.22597 s 18.13 Mpx/s 8.9 %
to 5478x3424 bil 0.58726 s 6.97 Mpx/s 11.7 %
to 5478x3424 bic 0.74648 s 5.49 Mpx/s 7.5 %
to 5478x3424 lzs 0.90867 s 4.51 Mpx/s 5.7 %I admit I was happy about the results. I managed to speed up the code 2.5 times, and you won’t have to use better hardware or anything like that to get the boost: the same number of cores of the same CPU. The only requirement was updating Pillow to the version 2.7.
There still was some time for the update to come out, and I wanted to test the new code on a server for which it was intended. I cloned the code, compiled it, and at first, I even got the feeling I got something wrong:
Operation Time Bandwidth
--------------------------------------------
320x200 bil 0.08056 s 50.84 Mpx/s
320x200 bic 0.16054 s 25.51 Mpx/s
320x200 lzs 0.24116 s 16.98 Mpx/s
2048x1280 bil 0.18300 s 22.38 Mpx/s
2048x1280 bic 0.31103 s 13.17 Mpx/s
2048x1280 lzs 0.43999 s 9.31 Mpx/s
5478x3424 bil 0.75046 s 5.46 Mpx/s
5478x3424 bic 1.22468 s 3.34 Mpx/s
5478x3424 lzs 1.70451 s 2.40 Mpx/sLolwut!?
Everything performed the same as before any optimization. I re-checked everything ten times and included prints to check if I was running the proper code. It wasn’t a side effect of Pillow or the environment: the problem could be easily reproduced even on a small code snippet of 30 lines.
I posted a question on StackOverflow, and in the end, I was able to discover such pattern: the code was slow if compiled with GCC for a 64-bit platform. And that was the difference between the systems running on my laptop (32-bit) and the server (64-bit) I cloned the code to.
Well, Glory to Moore, I was not crazy, it was a real bug in the compiler. Moreover, they fixed the bug in GCC 4.9, but GCC 4.8 was included in the current Ubuntu 14.04 LTS distribution. That is, GCC 4.8 was most likely installed by most users of the library. Ignoring this was impractical: how would users benefit from the optimization if it does not work in the majority of cases including the one it was made for.
I updated the question on StackOverflow and threw a tweet. That’s how Vyacheslav Egorov, a former V8 engine developer and a genius of optimization, came to help me.
To understand the problem, we’ll need to delve deeper into the history of CPUs and their current architecture. Way back, x86 processors did not work with floating-point numbers, x87 command set enabled coprocessors did that for them. Those would execute instructions from the same thread as CPUs but were installed on the motherboard as separate devices. Then, coprocessors were built into central ones and physically formed one device together. Sooner or later, in the Pentium III CPU, Intel introduced a set of instructions called SSE (Streaming SIMD Extensions). The third article of the series will be devoted to SIMD instructions, by the way. Despite its name, SSE did not only contain SIMD instructions for working with floating-point numbers but also their equivalents for scalar computations. That is, SSE held a set of instructions duplicating the x87 set but encoded and behaving differently.
However, compilers didn’t hurry to generate SSE code for floating-point calculations but would continue using the older x87 set. After all, the existence of SSE in a CPU could not be guaranteed while the x87 set was there for decades. Things changed when the 64-bit CPU mode was out. For this mode, the SSE2 instructions set became mandatory. So, if you write a 64-bit program for x86, the SSE2 instructions set is available for you at the least. And that’s what compilers make use of: they generate SSE instructions for floating point calculations in 64-bit mode. Again, I’m talking about ordinary scalar calculations, no vectorization involved.
That’s what was happening in our case: different instruction sets were used for 32-bit and 64-bit mode. However, this does not explain why the later SSE code worked many times slower than the outdated x87 one. To understand the phenomenon, let’s talk about how CPUs execute instructions.
Some time ago, processors did really “execute” instructions. They would get the instruction, decode it, execute what it was about, and put results where they were supposed to. Those could be smarter, and it happened. Modern processors are brainy and more complex: they consist of dozens of different subsystems. On a single core, without any parallel processing, CPUs execute several instructions in one clock cycle. This execution occurs at different stages for different instructions: while some are being decoded, another get data from the cache, others get transferred to the arithmetic block. Each processor subsystem deals with its part of instruction. That’s called a CPU pipeline.
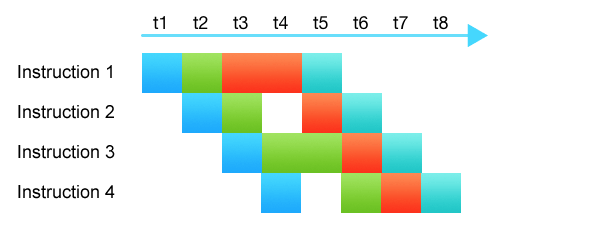CPU pipelineIn the picture, colors show different CPU subsystems. Even though instructions require 4–5 cycles to execute, thanks to the pipeline, each clock cycle one instruction can be started while another gets terminated.
The pipeline works the more efficiently, the more uniformly it is filled, and the fewer subsystems are idle. There even are CPU subsystems that plan the optimal pipeline filling: they swap, split or combine instructions.
One of the things causing CPU pipelines to under perform is data dependency. That’s when some instruction requires the output of another instruction to execute so that many processor subsystems are idle waiting for those outputs.
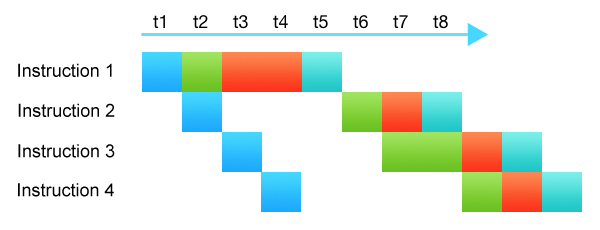A CPU pipeline where instruction two is waiting for the completion of the first one, and most subsystems are idleThe figure shows instruction two is waiting for the completion of the first one. Most subsystems are idle. This slows down the execution of an entire instruction chain.
And now, with all the info, let’s look at the pseudo code of an instruction converting an integer to a floating-point number:
Instruction: cvtsi2ss xmm, r32
dst[31:0] := Convert_Int32_To_FP32(b[31:0])
dst[127:32] := a[127:32]The results are written in the lower 32 bits. Even though it’s further written that lower bits from the register a are transferred to the dst register, it’s not what is happening.
Looking at the signature of the instruction, we get it only deals with a single xmm register which means both dst and a relate to the same register: higher 96 bits are not moving anywhere. And here’s where we have the data dependency. The instruction is made in such a way that ensures the safety of the high-order bits, and therefore, we need to wait for the results of all other operations working with the register to execute it.
However, the thing is we aren’t using any of the higher bits and are interested in the lower 32-bit float. We don’t care about the higher bits hence those don’t affect our results. That’s called a false data dependency.
Fortunately, we can break the dependency. Before executing the cvtsi2ss conversion instruction, the compiler should perform the registry cleanup via xorps. I can’t call this fix intuitive and even logical. Most likely, it’s not a fix but a hack on the decoder level that replaces xorps + cvtsi2ss with some internal instruction with the following pseudo code:
dst[31:0] := Convert_Int32_To_FP32(b[31:0])
dst[127:32] := 0The fix for GCC 4.8 is rather ugly; it consists of Assembler and a preprocessor code that checks if the fix can be applied. I won’t show the code here. However, you can always check out the commit 81fc88e. This completely fixes the 64-bit code. Here’s how it affects the performance on a server machine:
Operation Time Bandwidth
---------------------------------------------
320x200 bil 0.02447 s 167.42 Mpx/s
320x200 bic 0.04624 s 88.58 Mpx/s
320x200 lzs 0.07142 s 57.35 Mpx/s
2048x1280 bil 0.08656 s 47.32 Mpx/s
2048x1280 bic 0.12079 s 33.91 Mpx/s
2048x1280 lzs 0.16484 s 24.85 Mpx/s
5478x3424 bil 0.38566 s 10.62 Mpx/s
5478x3424 bic 0.52408 s 7.82 Mpx/s
5478x3424 lzs 0.65726 s 6.23 Mpx/sThe situation I described in this part of the series is rather frequent. The code that converts integers to floats and then runs some calculations can be found in almost any program. That’s also the case with ImageMagick, for instance: its 64-bit versions compiled with GCC 4.9 are 40% faster than the ones compiled using previous GCC versions. In my opinion, that’s a serious flaw in SSE.
That’s how we got to the average improvement of 2.5x without altering the approach: by using general optimizations. In my next article, I’ll show how to speed up that result 3.5 times by implementing SIMD techniques.
Ready to get started?
Join developers who use Uploadcare to build file handling quickly and reliably.